Here we report in detail the verification test of openQCM Quartz Crystal Microbalance in contact with pure water according to the theory based on Kanazawa – Gordon equation
THEORY
Kanazawa and Gordon derives a simple relationship [1][2], which expresses the frequency variation of a quartz crystal in contact with a liquid in terms of material parameters of the fluid and the quartz. The relationship is:
\Delta f = - f_0^{3/2} \cdot \left( \frac{\eta_L \rho_L}{\pi \mu_Q \rho_Q} \right)^{1/2}
where:
f_0 nominal vibration frequency of the dry quartz crystal
\eta_L absolute viscosity of the liquid
\rho_L density of the liquid
\mu_Q shear modulus of the quartz crystal
\rho_Q density of the quartz crystal
In other words, the frequency variation of a quartz crystal in contact with liquid depends on the viscosity – density product of the liquid under investigation. The Kanazawa – Gordon equation is verified under the following assumption:
i) quartz crystal is a perfectly elastic solid, which means energy dissipation due to crystal internal friction and mounting friction are neglected
ii) the liquid is Newtonian, which means it is a purely viscous liquid,
iii) the liquid can be approximated to a semi-infinite layer, which means the penetration depth of the shear wave inside the liquid is very much smaller than the liquid thickness in contact with the quartz crystal.
MATERIAL and METHODS
Two different openQCM instruments were compared in order to perform the verification test under liquid. It was used a 10 MHz AT-cut quartz crystal sensors with 6 mm diameter gold electrode. Pure water was injected in the openQCM measurement chamber using a syringe pump. The measurement chamber volume is roughly 30 µL (micro liters). The material parameters of the fluid and the quartz are:
f_0 \simeq 10 \, MHz
\eta_L = 1.002 \times 10^{-2} \, g \cdot cm^{-1} \cdot s^{-1} (T = 20^\circ )
\rho_L = 0.9982 \: g \cdot cm^{-3} (T = 20^\circ )
\mu_Q = 2.947 \times 10^{11}\, g \cdot cm^{-1} \cdot s^{-2}
\rho_Q = 2.648 \, g \cdot cm{-3}
According to Kanazawa Gordon equation the frequency variation from air to pure water is:
\Delta f = 2020 \, Hz
The frequency shift caused by injection of pure water in the measurement chamber was measured using the following procedure:
TIP and TRICKS
Here some tip and tricks for using openQCM in contact with liquid.
1. Holder and quartz crystal connection: pay attention to mount the quartz crystal into the openQCM holder (model HC-48/U) as shown in Figure 1
2. Bubble: please make sure no bubbles are present in the measurement chamber during your entire test. We have designed a transparent measurement cell exactly for this reason.
3. Liquid injection: in order to avoid bubble it is a good practice to inject the liquid in the measurement chamber, using a syringe pump, a peristaltic pump or whatever, as shown in Figure 2. You should use the larger hole as inlet (IN) and the smaller one as outlet (OUT).
4. o-ring mechanical stress: sometimes the o-ring can become more rigid when it is in contact with liquid, in particular for the first time. It causes a long-term drift in the frequency behavior. In this case, the mechanical stresses can be released by knocking hard with one finger on the measurement chamber.
5. Alignment: try to align at your best the quartz crystal electrode to the centre of the measurement cell. In this way the quartz crystal will be uniformly in contact with the liquid
EXPERIMENTAL SECTION
The experimental results of the entire test for both openQCM instruments are shown in Figure 3. The entire test verification takes approximately 2 hours.
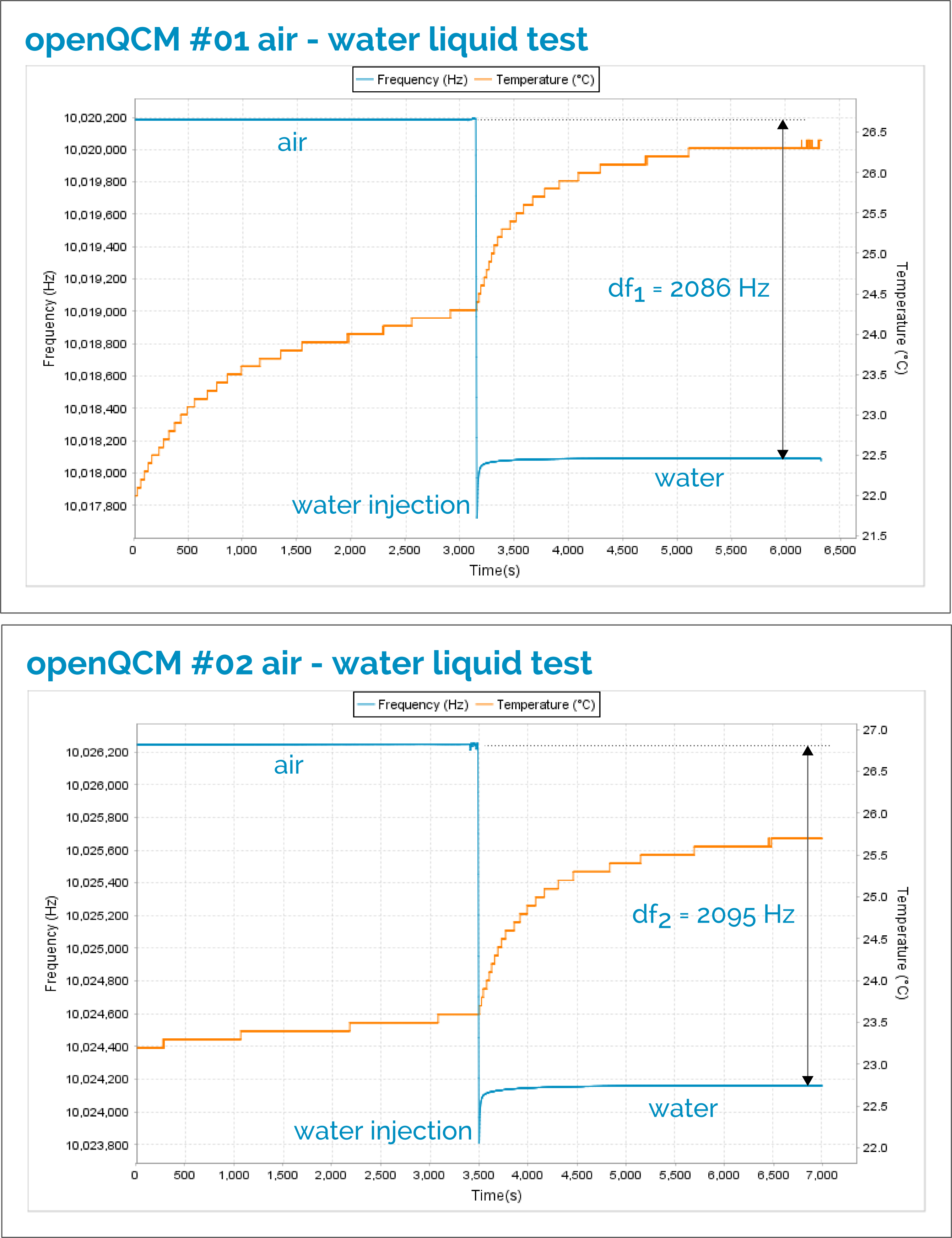
openQCM instrument #01
The initial frequency corresponds to the quartz crystal in contact with air. The initial frequency was measured on a time interval of about 30 minutes at temperature of about 23.5 °C. After the injection of pure water, it is necessary to wait for the new steady state. The final frequency corresponds to the quartz crystal resonator in contact with pure water. The final frequency was measured on a time interval of about 30 minutes at temperature of about 26.5 °C. The table below summarizes the experimental results for openQCM #01 instrument and the Figure 4 shows the frequency data set in air and liquid environment
| initial frequency (air) | f_{in} = 10026247.3 ± 0.2 Hz |
| final frequency (water) | f_{fin}= 10024160.8 ± 0.7 Hz |
| frequency difference | \Delta f = 2086.5 ± 0.7 Hz |
Table 1 Experimental results for openQCM #01 device: initial frequency corresponds to quartz crystal in contact with air, final frequency corresponds to quartz crystal in contact with liquid pure water
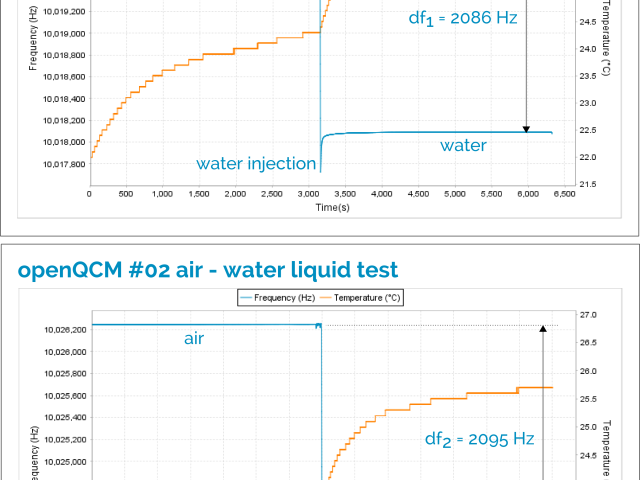
openQCM instrument #02
The same procedure was used for the second openQCM device. The initial frequency was measured on a time interval of about 30 minutes at temperature of about 24.0°C The final frequency was measured on a time interval of about 30 minutes at temperature of about 26.2 °C. The Table 2 below summarizes the experimental results for openQCM #02 instrument and Figure 5 shows the frequency data set in air and liquid environment
| initial frequency (air) | f_{in} = 10020185.6 ± 0.2 Hz |
| final frequency (water) | f_{fin}= 10018090.4 ± 0.4 Hz |
| frequency difference | \Delta f = 2095.2 ± 0.5 Hz |
Table 2 Experimental results for openQCM #02 device: initial frequency corresponds to quartz crystal in contact with air, final frequency corresponds to quartz crystal in contact with liquid pure water
RESULTS and CONCLUSION
The experimental results demonstrate a good agreement between the frequency shift measured by openQCM to the passage from air to pure water and the theoretical prediction of the Kanazawa Gordon equation. The theory predicts a frequency shift of about 2kHz for a 10 MHz quartz crystal resonator from air to pure water at ambient temperature. The frequency shift measured using openQCM is very close to the theoretical value. It was also demonstrated the openQCM measurement reproducibility by testing and comparing two different openQCM instruments under the same experimental conditions. The test and results we have reported shown a very simple and practical way to verify the working condition of openQCM and it is also a good way to make some practice with quartz crystal microbalance in contact with liquid.
FURTHER READINGS
Kanazawa and Gordon published their theoretical and experimental results in two papers in the ’80s. The papers are pioneering and inspiring masterpiece in this field. You should read them!
[1] K Keiji Kanazawa and Joseph G Gordon II, “Frequency of a quartz microbalance in contact with liquid”, Anal. Chem., 1985, 57 (8), pp 1770–1771
doi: 10.1021/ac00285a062
[2] K Keiji Kanazawa and Joseph G Gordon II, “The oscillation frequency of a quartz resonator in contact with liquid”, Analytica Chimica Acta, Volume 175, 1985, Pages 99-105
doi:10.1016/S0003-2670(00)82721-X
enjoy,
marco
